싱그럼의 연구실
[끝말잇기] 승리 음절, 패배 음절, 순환 음절 분류 알고리즘 본문
설명
1. 끝말잇기를 구현한 이진 유향 그래프에서 간선의 방향을 모두 바꾼다. 각 음절에 내차수(음절로 들어가는 간선의 수)와 외차수(음절로부터 나오는 간선의 수), 카운터(음절의 외간선 중 승리 음절로부터 나온 간선의 수)를 할당한다. 처음 상태에서 승리 음절로 분류된 음절은 없으므로 모든 음절의 카운터는 0이다.
순환 음절 집합 \(C\)와 집합열 \(L_0, L_1, L_2, ...\)과 \(W_0, W_1, W_2, ...\)를 만든다.
\(C\)에 모든 음절을 넣는다.
2. \(n := 0\)
3. \(C\)에서 '내차수 = 카운터'가 되는 음절을 \(L_n\)에 옮긴다. 만약 이러한 음절이 없다면 7로 이동
4. \(L_n\) 내의 모든 음절들에 대해 그 음절에서 나온 간선에 연결된 음절들을 \(C\)에서 \(W_n\)로 옮긴다.
5. \(W_n\)의 모든 음절들에 대해 그 음절에서 나온 간선에 연결된 음절들에 카운터를 1씩 증가시킨다.
6. \(n := n+1\), 3으로 돌아간다.
7. 반복을 멈춘다.
8. \(C\)는 순환 음절 집합, \(L = L_0\cup L_1\cup L_2 \cup ...\)는 패배 음절 집합, \(W = W_0 \cup W_1 \cup W_2 \cup ...\)는 승리 음절 집합으로 분류가 끝났다.
예시
다음과 같은 유향 그래프를 생각해보자.

그래프의 간선의 방향을 모두 바꾼다.

정점에 카운터를 적어 넣는다.

내차수 = 카운터인 정점을 찾는다. 그리고 그것들에 \(L_0\)을 적어 넣자.

\(L_0\)에 인접하게 이어지는 정점은 \(W_0\)이 된다.

각 \(W_0\)점들에 대해 그것이 가리키는 정점에 카운터를 1씩 더한다.


내차수 = 카운터인 음절을 찾고 그것을 \(L_1\)로 표시하자.

\(L_1\)에서 인접하게 이어지는 정점은 \(W_1\)이 된다.

\(W_1\)에 대해서 그것에 이어지는 정점에 카운터를 1씩 증가시킨다.

내차수 = 카운터인 음절을 찾고 그것을 \(L_2\)로 표시한다.

\(L_2\)에서 이어지는 정점은 \(W_2\)가 된다.(없음)
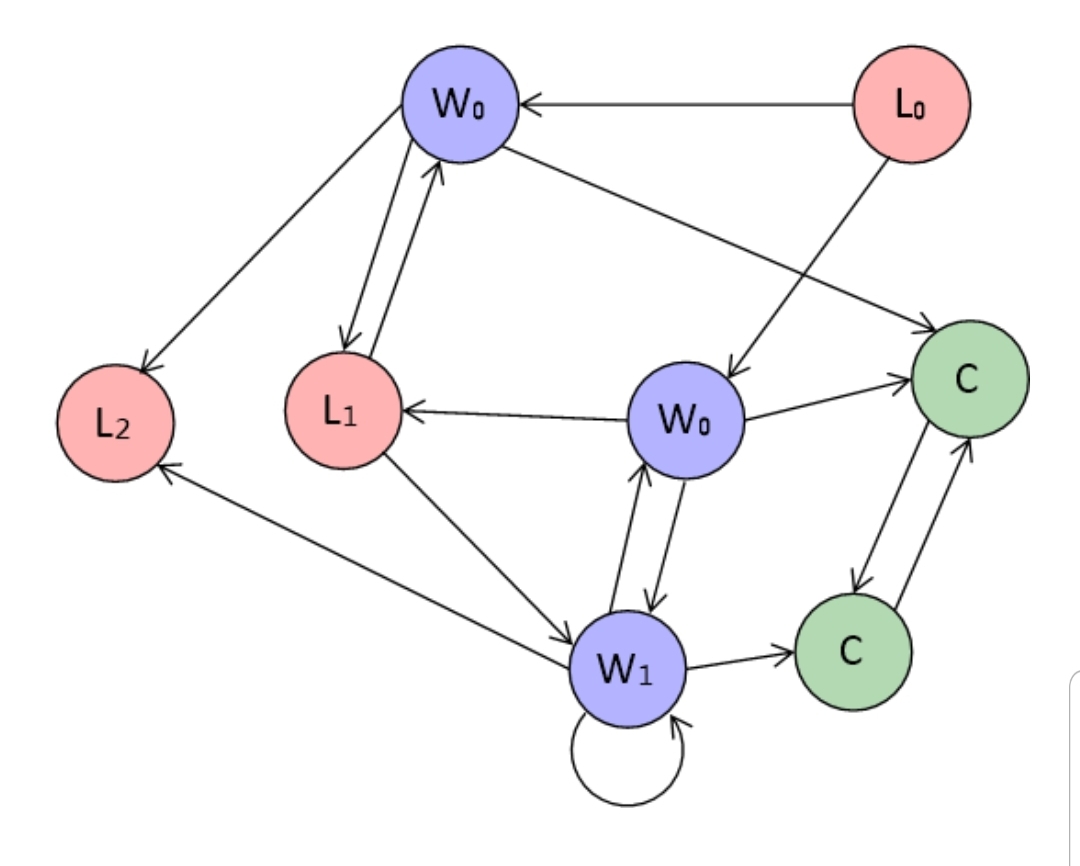
더 이상 카운터 = 내차수를 만족하는 정점은 남아있지 않으므로 반복을 멈추고, 남은 음절에 C를 표시한다.


이렇게 주어진 유향 그래프에서 승리, 패배, 순환 음절 분류가 끝났다.
'끝말잇기 > 이론' 카테고리의 다른 글
| [실험] 깊이 심화 탐색으로 끝말잇기 분석하기 (5) | 2024.11.01 |
|---|---|
| [끝말잇기] 단어 검색 웹앱을 만들었습니다 (1) | 2022.09.11 |
| [끝말잇기] 무향 끝말잇기를 유향 끝말잇기로 구현하는 그래프 패턴 (0) | 2022.07.22 |